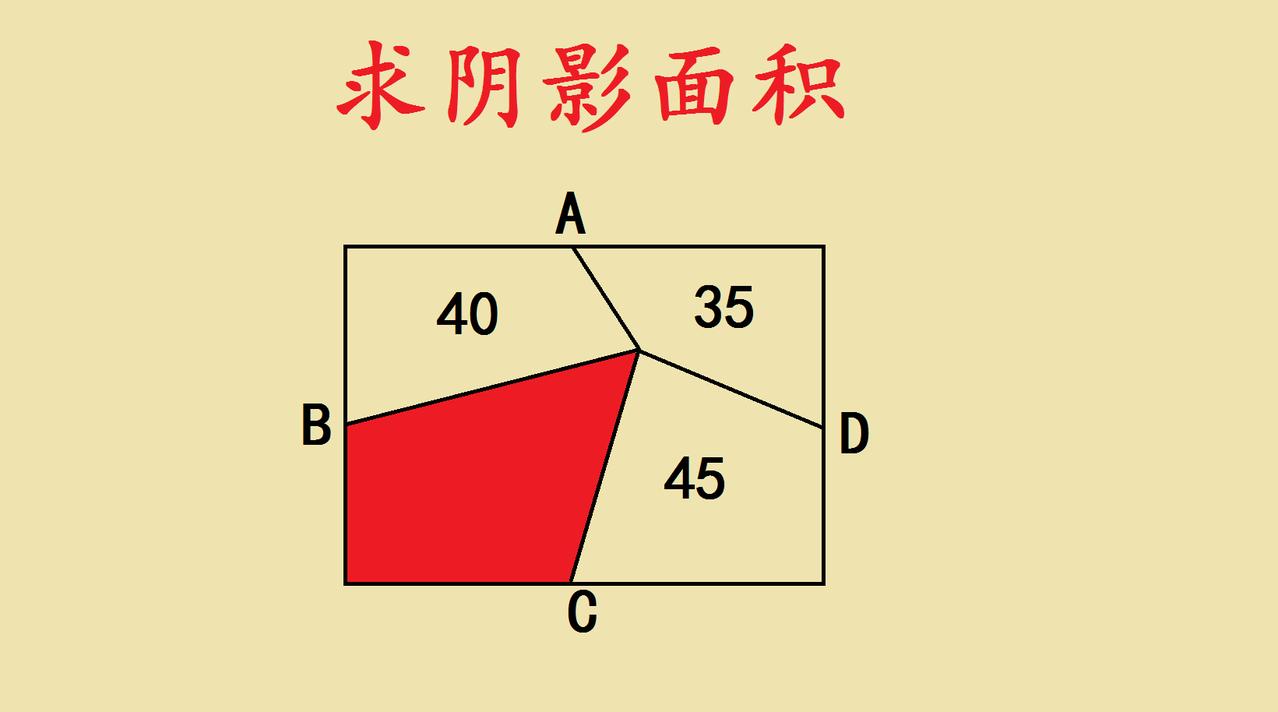
核心方法：等高模型 原理：三角形面积=底×高÷2，若两个三角形底边相同且“顶

核心方法：等高模型 原理：三角形面积=底×高÷2，若两个三角形底边相同且“顶点到对应底边的垂直距离（高）”相等，则面积相等。 长方形中的隐藏条件： - 中点将边分为等长线段，设长方形长为2a、宽为2b，各中点分边后每段长a或b。 ​ - 对角线交点O到四边距离相等（长方形中心性质），形成多组等高三角形。 解题步骤 1️⃣ 标注区域：设阴影面积为S，四个三角形分别为①(40)、②(35)、③(45)、④(S)。 2️⃣ 构建等高模型： - 连接长方形上下边中点，将图形分为上下两个小长方形，每个小长方形内的两个三角形同底等高（高均为b/2）。 ​ - 可得：①+③=②+④（上下两部分面积之和相等，均为长方形面积的一半）。 3️⃣ 代入计算：40+45=35+S → S=50。 学霸思维总结 ✅ 关键突破：不纠结具体边长，利用“等高模型”转化面积关系，避免复杂方程。 ✅ 易错点：忽略中点与中心的等高性质，陷入“求边长”的思维误区。 ✅ 拓展：正方形、平行四边形中也可应用类似模型，记住“同底等高面积等”是几何解题黄金法则！